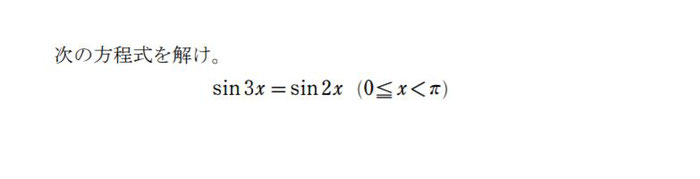1. ホーム
  2. ゴロ開発研究所
  3. 数学のゴロ
  4. 三倍角の公式の覚え方

【語呂合わせ】三倍角の公式の覚え方

3倍角の公式の覚え方
3倍角の公式の覚え方

一見、数Ⅱの三角関数は覚える公式が多いように感じますが、実は違います。

三倍角の公式はSinだけゴロで簡単に覚えて、それ以外は覚える必要はありません。

さて、3倍角の公式の語呂合わせと言えば、サンシャイン良美が古典的なゴロとして有名ですが、ZOOM医進館のゴロは符号の情報が追加されている上に更に覚えやすく、上位互換のゴロと言えます。

ZOOM医進館のゴロでサクッと覚えて、どんどん使いこなして、変形後のイメージが楽に見える状態にしましょう。

では、本邦初公開です。

３歳はダメ４歳は見事

３歳（Sin）はダメ（ー）４歳（Sin）は見（３乗）事

片方のSINだけ覚えて、COSはSINの前半部分と後半部分を入れ替えた形です。

ちなみに、この片方だけ覚えるテクニックは記憶術の定番のひとつです。

三倍角の公式の覚え方（SINからCOS）
三倍角の公式の覚え方（SINからCOS）

短期記憶の並べ替えクイズを用意しています。

瞬間記憶力テストにワープ

このページの最後に例題を用意してます。Youtube解説動画あり。

ハイレベル例題にワープ

瞬間記憶力テスト

（１）SINの三倍角の公式を正しい順番に並べ替えなさい。
　
  • －
  • ＝
  • ４
  • Sin３θ
  • ３
  • Sinθ
  • Sin３θ

（２）COSの三倍角の公式を正しい順番に並べ替えなさい。
　

  • Cos３θ
  • ３
  • ＝
  • Cosθ
  • Cos３θ
  • －
  • ４

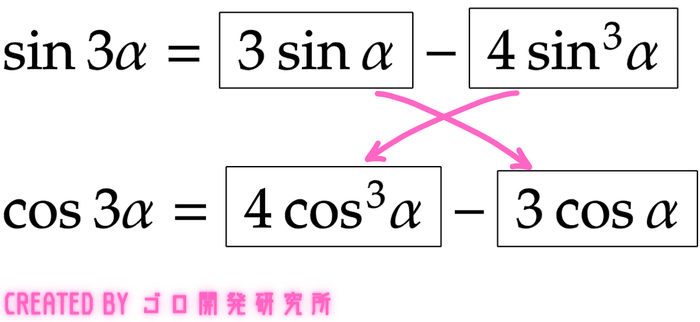
SINとCOSの３倍角の公式

Sin3θの公式です。

Sinの三倍角の公式の証明方法はこちら

sin 3 𝛼 = 3 sin 𝛼 − 4 sin 3 𝛼

Cos3θの公式です。

Cosの三倍角の公式の証明方法はこちら

cos 3 𝛼 = 4 cos 3 𝛼 − 3 cos 𝛼

tan（タンジェント）の３倍角の公式

Tan3θは無理せずに導出します。

二倍角の公式の覚え方の迅速導出法で関数を省略して変形をスピードアップ出来ますので、慣れてきたら以下の変形も大した変形にならないです。

関連記事
3倍角の公式（tan）
3倍角の公式（tan）

三角比の相互関係の公式の証明

1 cos 2 𝛼 ⇨ １ を 有 名 公 式 で 変 形 三 角 比 の 相 互 関 係 sin 2 𝛼 + cos 2 𝛼 = 1 = cos 2 𝛼 + sin 2 𝛼 cos 2 𝛼 = cos 2 𝛼 cos 2 𝛼 + sin 2 𝛼 cos 2 𝛼 = 1 + tan 2 𝛼 ⇨ 移 項 す れ ば tan 2 𝛼 の 形 で 変 形 可 tan 2 𝛼 = 1 cos 2 𝛼 − 1

三倍角の公式の求め方（証明）

一般的な三倍角の公式の証明方法と省略表記法、ドモアブルの定理の方法の3通りを紹介。

SINの証明

SINの３倍角の公式の証明です。

加法定理 → 2倍角の公式 → 三角比の相互関係を順に使いながら式を整理して導出します。

関連記事
sin 3 𝛼 = sin ( 2 𝛼 + 𝛼 ) 加 法 定 理 sin ( 𝛼 + 𝛽 ) = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽 = sin 2 𝛼 _ cos 𝛼 + cos 2 𝛼 _ sin 𝛼 2 倍 角 の 公 式 sin 2 𝛼 = 2 sin 𝛼 cos 𝛼 cos 2 𝛼 = cos 2 𝛼 − sin 2 𝛼 = 2 sin 𝛼 cos 𝛼 _ cos 𝛼 + ( cos 2 𝛼 − sin 2 𝛼 _ ) sin 𝛼 = 2 sin 𝛼 cos 2 𝛼 _ + ( cos 2 𝛼 _ − sin 2 𝛼 ) sin 𝛼 三 角 比 の 相 互 関 係 sin 2 𝛼 + cos 2 𝛼 = 1 cos 2 𝛼 = 1 − sin 2 𝛼 = 2 sin 𝛼 ( 1 − sin 2 𝛼 ) _ + ( 1 − sin 2 𝛼 _ − sin 2 𝛼 ) sin 𝛼 = 2 sin 𝛼 ( 1 − sin 2 𝛼 ) + ( 1 − 2 sin 2 𝛼 ) sin 𝛼 = 2 sin 𝛼 − 2 sin 3 𝛼 + sin 𝛼 − 2 sin 3 𝛼 = 3 sin 𝛼 − 4 sin 3 𝛼

COSの証明

同様に、COSの３倍角の公式の証明です。

cos 3 𝛼 = cos ( 2 𝛼 + 𝛼 ) 加 法 定 理 cos ( 𝛼 + 𝛽 ) = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽 = cos 2 𝛼 _ cos 𝛼 − sin 2 𝛼 _ sin 𝛼 2 倍 角 の 公 式 sin 2 𝛼 = 2 sin 𝛼 cos 𝛼 cos 2 𝛼 = cos 2 𝛼 − sin 2 𝛼 = ( cos 2 𝛼 − sin 2 𝛼 _ ) cos 𝛼 − ( 2 sin 𝛼 cos 𝛼 _ ) sin 𝛼 = cos 3 𝛼 − sin 2 𝛼 _ cos 𝛼 − 2 sin 2 𝛼 _ cos 𝛼 三 角 比 の 相 互 関 係 sin 2 𝛼 + cos 2 𝛼 = 1 sin 2 𝛼 = 1 − cos 2 𝛼 = cos 3 𝛼 − ( 1 − cos 2 𝛼 _ ) cos 𝛼 − 2 ( 1 − cos 2 𝛼 _ ) cos 𝛼 = cos 3 𝛼 − cos 𝛼 + cos 3 𝛼 − 2 cos 𝛼 + 2 cos 3 𝛼 = 4 cos 3 𝛼 − 3 cos 𝛼

省力型

省力型で、2倍角の公式の迅速導出法も使いながら導出します。

COSもTANも同様に証明して下さい。

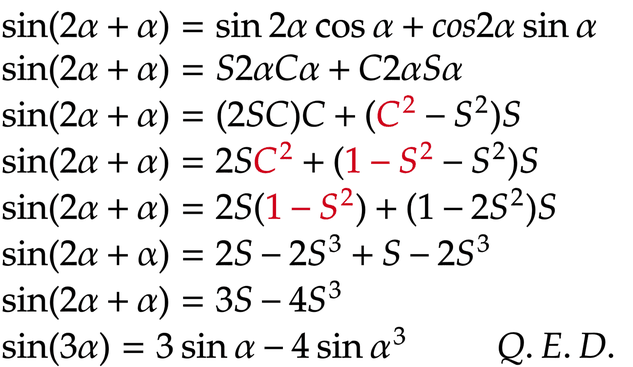
３倍角の公式の証明
３倍角の公式の証明

ドモアブルの定理で証明

Nに３を代入して展開して整理すれば導出できます。

演習代わりにCOS3ΘとSIN3Θ導出してみてください。

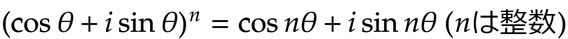
ドモアブルの定理
ドモアブルの定理

三倍角の公式のハイレベル例題

以下は難関大学レベルの例題です。解説は数学モンスターの動画を見てください。

さあ！今日から三倍角の公式をドンドン使おう！

練習問題１

練習問題１
練習問題１

練習問題1の解説

練習問題2

3倍角の公式練習問題２
3倍角の公式練習問題２

練習問題2の解説